A medencés és tavi haltermelés erőforrásai: a takarmányozás alapegyenlete - módosított 1985-ös modell

Csengeri István¹, Ruttkay András¹, Zsigri András¹, Zsigri Csilla¹, Horváth László², Péteri András¹

¹NAIK Halászati Kutatóintézet, Szarvas
²Szent István Egyetem, Halgazdálkodási Tanszék, Gödöllő

Kivonat

Az erőforrás kifejezés Ruttkay András "produkciós biológia" fogalma, illetve az általa használt „termelésbiológiai labor” név szerepel a címben. Az "erőforrás" fogalom is tulajdonképpen csak a produkciós biológiai kontextusban lesz tárgyalva az előadásban. A hidrológia, limnológia és a közgazdaságtan további aspektusaira csak röviden utalunk bevezetésben. 

A halastavak népesítés - takarmányozás - hozam viszonyainak értékelésre 1985-ben alkalmaztuk SGR-SFR telítési görbe y=a*x/(b+x) értelmezési tartományát kiterjesztve a

N (halastavi hozam) = a*x*(y+y₀)/(y+y₀+b*x)+c*x

takarmányozástani összefüggésekre épülő egyenlet szerinti hozam számítási modellt, melyben az „N” a nettó hozam, „x” a kihelyezési tömeg, „y” a takarmány mennyiség, „y₀” a természetes táplálék takarmány egyenértéke (tak. ekv.); „a” a növekedési potenciál, „c” az éhezési veszteség és „b” a fenntartó takarmány szükséglettel, valamint az „a” és „b” állandókkal arányos konstans (nyomtatásban csak kivonat jelent meg: Péteri, A. és mtsai., 1986. )

Az 1986-os és az 1992-es HAKI Napokon a témában előadott modellek nem arattak átütő sikert. Az AQUAMAX és az ARRAINA projektekben viszont már felmerült annak kérdése, illetve szükségessége, hogy magyarázattal szolgáljunk a természetes hozam meghatározására. Az újabb nekifutások (2015-ös, 2016-os HTT előadások, poszterek) sem találtak kedvező fogadtatásra, ezért a szerzőtársak már megjelent publikációit (Ruttkay A.,1990; Csengeri I. és mtsai. 1992; Csengeri I, 1996), valamint a szakirodalomból megismerhető adatokat, ábrákat újra áttekintve véglegesítettük későbbi egyenleteinket.

Mindannyiunk előtt ismeretes, a halak a felnőtt (szaporodóképes kornak megfelelő) testtömeg elérése előtt, s ezután is (bár ekkor már valamivel lassúbb) folyamatos, erőteljes (exponenciális) növekedésre képesek – hasonlóan Monod baktériumaihoz (Monod, J. 1949). A jelenséget a

w_t=w₀*e^^g*t (dw/dt= e^^g*t ),   

a gyakorlatban is igazolt egyenlettel lehet leírni, ahol az egyenletben a „w₀”=a kezdeti testtömeg, a w_t=a „t” időtartamú növekedési vizsgálat végén mért testtömeg és a „g” a specifikus növekedési erély (angolul: Specific Growth Rate – SGR), amit általában a növekedési görbe természetes („e”-alapú) logaritmusa alapján szokásos megadni %/nap-ban, vagyis 100 grammra, vagy 100 kg-ra és 1 napra vonatkoztatva az adott táplálási, takarmányozási körülményekhez:

SGR=100*(ln w_t - ln w₀)/t.

 A gyakorlati tapasztalat szerint a különböző takarmányozási körülmények esetén a „g” vagy „100*g” (SGR) telítési típusú függvénye a szintén %/nap-ban kifejezett takarmányozási rendnek, a takarmányozási „rátá”-nak (R%); pontosabban a takarmányhasznosítást is befoglaló SFR-nek, a specifikus takarmányozási rátának (angolul: Specific Feeding Rate – SFR=FCR*SGR ). 

Itt kell megjegyezni, hogy Ruttkay András szerzőtársunk – aki már nincs közöttünk – a %-os összefüggés helyett a g/kg/nap-ra vonatkoztatva javasolta használni az SGR és SFR értékeket 1990-es cikksorozatában (Ruttkay A., 1990a. Halászat, XXXVI (83), 46-49.). Mi a továbbiakban a gyarapodást kg kg^-1 nap^-1, illetve kg per kg a vizsgált periódus egészére vonatkoztatva használjuk az összefüggés halastavi alkalmazásának megkönnyítéséhez.

A telítési görbék hiperbolikus függvényekkel írhatók le, amelyekkel a halastavi takarmányozás „kicsit” bonyolultabban tervezhető, mint a jelenlegi gyakorlatban is használt lineáris halhozam-számítási módszer. Mi 1985-ben az enzimológiából ismert telítési görbe egyenletet: y=a*x/(b+x) választottuk, amit az éhezési taggal bővítettünk: y=a*x/(b+x) + c*x.  Az alapegyenlet könnyen értelmezhető az enzim reakciók sebességi viszonyait (kinetikáját) leíró, az enzimek (E) és a működésükhöz szükséges alapanyagok (szubsztrát vegyületek, S) és a termék (P) képződésének részfolyamatait leíró sémával:

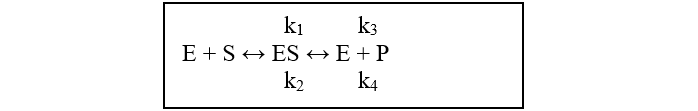
A folyamatban a k₁ és k₂, sebességi állandók az enzim-szubsztrát komplex (ES) egyensúlyi folyamatának oda-vissza alakulási sebességét jellemzik. Egyensúlyban a termék (P) képződését a k₁ és k₃ állandó határozza meg, mivel az egyensúlyra vezető bonyolult folyamat állandósult állapotában („steady state”) az E+P visszaalakulásának (k₄) ES komplexszé igen csekély, és az enzimek számára állandóan rendelkezésre áll a megfelelő „S” szubsztrát molekula. Az időbeni változást a koncentrációk kémiai reakció kinetikai egyenletei írják le. Ezeket itt nem részleteznénk, csak azt a nagyon fontos körülményt hangsúlyozzuk, hogy az alábbi (A) és (B) végeredmények arra az esetre vonatkoznak, amikor az [ES] koncentrációk „steady state”, állandósult egyensúlyi állapotban vannak, ez ugyanis az exponenciális növekedés alapja) következő egyenletek alapján.

(A):   v = k₃.[E]*[S]/(K_M + [S])        (B):  v = v_max.[S]/(K_M + [S]).        

(Ezek lényegében azonos egyenletek, mivel k₃*[E] = v_max.)
A (B) egyenletnek megfelelő formulát – tulajdonképpen a Michaelis‑Menten egyenletet – alkalmazta Monod a baktériumok (számbeli) növekedésének matematikai leírására (Monod, J. 1949). Monod képletét többször próbálták módosítani, pl. az alábbi egyenletekkel, melyeket Panikov hivatkozásai alapján ismerhetünk,(Panikov, N.S., 2011) ismerhettünk meg:

                      (C)  µ = µ_max*(1- e^(-K_s*S))    (Mayberry W.R. és mtsai., G. 1967)   
                      (D)  µ = µ_max*S^ⁿ /(K_s + S^ⁿ)                         (Moser, H. 1958)              
                      (E)  µ = µ_max*S^ⁿ /(K_s*x+S^ⁿ)                       (Teissier, G. 1956)           

A fenti (C) egyenlet tulajdonképpen azonos tartalmú a hidrobiológiában alkalmazott 1945-ös Ivlev-féle formulával:

                      (F)  G=G_max*(1-e^{^(- b*C)}),                               (Ivlev, V.S. 1945)                

csak míg a (C)-ben a limitáló tápanyag koncentrációja, az (S),  Ivlevnél a „C” a plankton fogyasztás szerepel független változóként.

A fenti (A), (B) (az A-nál és B-nél az n-kitevő egyenlő eggyel) és (D) egyenlet tulajdonképpen azonos formájúak a Hill-egyenlettel (Hill, A.V. 1910), amit az enzim kinetikai vizsgálatoknál olyan esetekben alkalmaznak, amikor a több alegységből álló (pl. dimer-, tetramer- oligomer-) makromolekulákhoz (általában fehérjékhez) kapcsolódó ligandum, vagy szubsztrát előtt már más ligandum is kötődik ugyanazon makromolekulához egy más helyen úgy, hogy közben megváltozik a molekula térszerkezete az allosztérikus átalakulás révén („allosteric transition”). Ezt nevezik „cooperative binding”-nak, kooperativ kötődésnek. Tulajdonképpen az ilyen jelenséggel kapcsolatos folyamatok jellemzésére alakult ki az MWC-modell (az MWC a Monod‑Wyman‑Changeux szerzői hármas nevének kezdőbetűiből alkotott rövidítés), amivel pl. a hormonok, gyógyszerek, drogok és a limitáló tápanyagok biokémiai, élettani hatását is le lehet írni.          

Az (A) és (B) egyenleteket, mint növekedési modelleket a Hill-egyenlet alakjában felírva

v = k₃.[E]*[S]^ⁿ/(K_M + [S]^ⁿ), ill. v = v_max *[S]^ⁿ/(K_.5^{^n} + [S]^ⁿ)

az egyenletek tulajdonképpen kifejezik a baktériumoknak, a halaknak a fentiekben már említett exponenciális növekedési képességét. Azt az alkalmazkodó (adaptációs) képességet, ami növekedés auto-katalitikus sajátosságaiban rejlik, ugyanis a növekedés során a biomasszában növekszik az enzimek mennyisége és a nagyobb enzim mennyiséghez több szubsztrátra van szükség a telítés eléréséhez. Tulajdonképpen a v = k₃.[E]*[S]^ⁿ/(K_M + [S]^ⁿ) egyenlet rejti burkoltan magába azokat az „erőforrásokat”, melyek miatt az előadás címét így fogalmaztuk meg.

A k₃ állandó nem egy enzimre vonatkozik a baktériumoknál (Monod, J. 1949), s a még összetettebb biológia „rendszerben” – amit egy hal egyed képvisel – még bonyolultabb a helyzet, így a k₃ állandó egy olyan enzim vagy enzim rendszer jellemzője, aminek aktivitása állandó, és az adott rendszerben a növekedés limitáló tényezője a hozzátartozó tápanyag ellátás limitáló jellegénél fogva. Ennek megfelelően kell biztosítanunk azt a tápanyag ellátást, ami biztosítja a növekedést meghatározó enzim állandósult telítettségét, vagyis az exponenciális növekedést. A halaknál általában a fehérje, illetve az abban jelenlévő aminosavak közül az első limitáló esszenciális aminosav (IEAA) a limitáló tápanyag. Ha más tápanyag (pl. C-vitamin, B₁-vitamin stb.) a növekedés limitáló tényezője, akkor más enzim, enzimrendszer határozza meg a növekedés sebességét. A genetikailag meghatározottan az enzim rendszerek k₃ állandóik képviselik az 1. erőforrást.

Az enzimek mennyiségének exponenciális növekedése és annak adaptív jellege (enzim indukció) a kihelyezett halak biomasszájában – az E enzim koncentráció változatlansága, s esetleges csekélyebb csökkenése esetén is – egy 2. erőforrást képvisel. Ennek az erőforrásnak a növeléséhez járul hozzá a nemesítés és a szelekció.

A halastavaknál a takarmány felvételből, valamint az elfogyasztott természetes táplálékból származó S szubsztrát tápanyagok koncentrációja képviseli a 3. és 4. erőforrást. Külön erőforrásokként lehet megnevezni azokat a tavi termelésbiológiai és tenyésztés technológiai beavatkozásokat, amelyekkel kedvezően módosítható a felvehető (elfogyasztott) természetes táplálék mennyisége, s amelyekre különös figyelmet kell fordítanunk a jövőben a hal termelés növeléséhez.

Ruttkay András kollégánk megfigyelései és levont következtetése, amit leegyszerűsítve úgy fogalmazott meg: „nem mindegy, hogy mit nem eszik a hal” hívja fel a figyelmünket arra, hogy fenntartó táplálék mennyiség alatti takarmány adagoknál is vizsgálatok szükségesek, amit ő külön el is végzett (Ruttkay A. 1990a,b,c), s amit néhány szakirodalmi leírásban is láthatunk. Az itt elemzendő, 1996-ban publikált (Csengeri I. 1996) mérési eredmények választ adhatnak azokra az éhezési tömegveszteséggel kapcsolatos kérdésekre, melyeket Ruttkay András kolléga külön tárgyalt az 1990-es cikksorozatában.

A fenti enzimológiai háttér áttekintését követően a patkányok táplálék, illetve tápanyag felvételének és a növekedésének összefüggésére vonatkozó, Mercer és munkatársai által elért vizsgálati eredmények (Morgan et al., 1975. Proc. Nat. Acad. Sci. USA 72(11):4327-4331; Mercer, L.P. 1982. J. Nutr., 112(3):560-6) birtokában kezdtünk az 1985-ös modell megújításához. A mi takarmányozástani modellünk alapja tulajdonképpen a fenti (A) és (D) modell, amit Mercer és munkatársai is alkalmaztak.

Először Csengeri István 1996-ban megjelent publikációjában (Csengeri, I. 1996) lévő takarmányozási és növekedési adatokat elemeztük. Ott az SFR és SGR adatok a szokásos százalékos módon vannak megadva, de a kiadagolt összes takarmány, illetve a kezdeti és végső egyedi tömegek is szerepelnek. Így könnyen modellezhető volt a kg/kg/nap SFR-SGR adatok által meghatározott görbe, valamint az FCR és FER adatok. A modellezésnél az alábbi egyenletet alkalmaztuk:

SGR =- c*x + a*x*(y)^ⁿ/(y^ⁿ+(b^ⁿ*x^ⁿ)

ahol az x=SFR, az a ,b, c, és n a meghatározandó paraméterek a fentiekben már említett tartalommal: „a” a növekedési potenciál, „c” az éhezési veszteség és „b^{^n} = K_.5^{^n} = K_I” a fenntartó takarmány szükséglettel, valamint az „a” és „c” állandókkal arányos konstans, amihez Mercer és munkatársaihoz hasonlóan mi is bevezettük K_.5^{^n}=K_I táplálék felvétel („Intake”) kinetikai állandót a szélsőértékek meghatározásához.

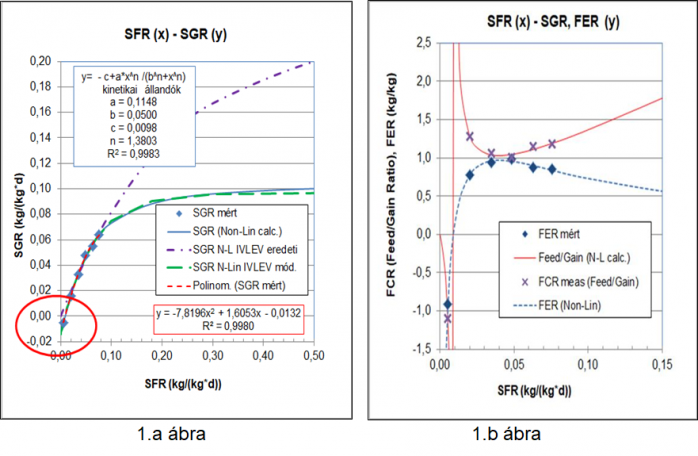
Csengeri István adatait elemezve jutottunk az 1.a és 1.b ábrákon bemutatott összefüggésekhez. Csengeri 3. táblázatában bemutatott adatok (Csengeri I., 1990) olyan kísérletből származnak, amelyben a 10 g körüli átlagos testtömegű pontyok napi takarmány adagja nem hetenkénti periódusokra, hanem a napi növekedést is figyelembe vevő módon lett meghatározva. Ezért magas SGR értékeket kaptunk, a legmagasabb érték a szokásos napi %-ban kifejezve 7,57 kg/100 kg/nap SFR értéknél az SGR 6,42 kg/100 kg/nap-ot. Ezen túlmenően, a fenntartó szint alatti takarmányozás is történt, amely biztosította a növekedés nem csak a pozitív irányú adaptáció, de a fenntartó szint alatti lassuló fogyáshoz való adaptáció is megtörténhessen. Ez igazolja azt, hogy ebben a takarmányozási rendszerben sikerült a növekedés és a fogyás sebességét meghatározó enzim rendszert, enzim rendszereket „steady state” állapotban tartani. Az 1. ábrán bemutatjuk az ugyanezen adatokra a alkalmazott Ivlev-féle egyenlet, illetve annak egy éhezési tömeg veszteség taggal kibővített változatának jó illeszkedését a mért adatokra (1.a ábra). A határérték felé közeledve viszont már szembetűnőek a különbségek az eredeti Ivlev-egyenlet alkalmazásakor. Az eredeti Ivlev-egyenletre vonatkozó görbe egyfajta magyarázatul szolgál arra, hogy miért vizsgálták külön korábban a népesítés‑hozam és a takarmányozás‑hozam összefüggéseket.

Ruttkay András hasonló, 10 g körüli kezdeti testtömegű 10,0 kg/100 kg/nap SFR értéknél 2,55 kg/100 kg/nap adatokat kapott (Ruttkay, A. 1990a, 1. ábra). Ezek az adatok olyan kísérletből származnak, amelyben a 10 g körüli átlagos testtömegű pontyok napi takarmány adagja hetenkénti periódusokra lett kiszámítva. Ebben a takarmányozási rendszerben nem sikerült a növekedés sebességét meghatározó enzim rendszert, enzim rendszereket „steady state” állapotban tartani, tulajdonképpen egy váltakozó fel-le szabályozás („up and down regulation”) történt meg. Összevetve ezeket az adatokat az előző Csengeri-féle adatokkal, ahol folyamatos volt az „up-regulation” (itt nem közölt ábrák) egyértelmű a folyamatos magas jó tápanyag ellátás előnye a gyors növekedést biztosító „steady state” állapot megvalósításához. Nagyobb halaknál elvileg még megengedhető lenne a hetente‑2-hetente történő mérésekhez igazítani a napi takarmányadagokat, de bizonyosan ott is a napi növekedést figyelembe vevő módszer a célravezető. 

Ruttkay András szintén 10 g körüli kezdeti testtömegű pontyoknál búza etetésnél 2,9 kg/100 kg/nap SFR értéknél 0,58 kg/100 kg/nap adatokat kapott, s már 1,97 kg/100 kg/nap SFR értéknél megközelítette a telítési szakaszt (Ruttkay, A. 1990a, 3. ábra). Az intenzív tartásnál egyértelműen fehérjeszegény takarmánynak számító búza etetésével Ruttkay közelítőleg csak 1/5-nyi tömeggyarapodást ért el azonos takarmányozási szintnél a tápos csoportjához viszonyítva. Ez Csengeri tápos csoportjához viszonyítva csak 1/10-nyi gyarapodás, ami szintén a „steady state” állapot megvalósításához szükséges etetési rendszer és a jó takarmány etetésének előnyét igazolja.

Fentebb említettük, hogy az 1985-ös modellnél abból a felismerésből indultunk ki, hogy kétszer, háromszor… annyi halnak kétszer, háromszor… annyi a létfenntartásához, gyarapodásához, növekedéséhez az energia és tápanyag szükséglete, mint pl. 10 darab vagy 1 kg halnak.                             
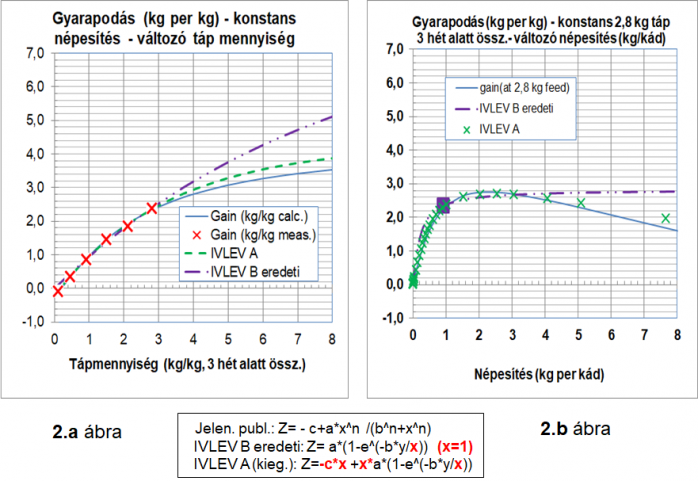
Ezt a  mindenki számára nyilvánvalónak látszó összefüggést igazolja a 2.a és 2.b, ábra, melynek állandóit a                      

gyarapodás 3 hét alatt =- c*x + a*x*(y)^ⁿ/((y)^ⁿ+(b^ⁿ*x^ⁿ)
gyarapodás 3 hét alatt =- c*N*w0 + a* N*w0 *(y)^ⁿ/((y)^ⁿ+(b^ⁿ* N*w0 ^ⁿ)

egyenletek alapján paramétereztük.

A két ábra egyértelműen mutatja, hogy takarmányozás‑hozam összefüggés két különböző nézete ugyanannak a függvénykapcsolatnak.

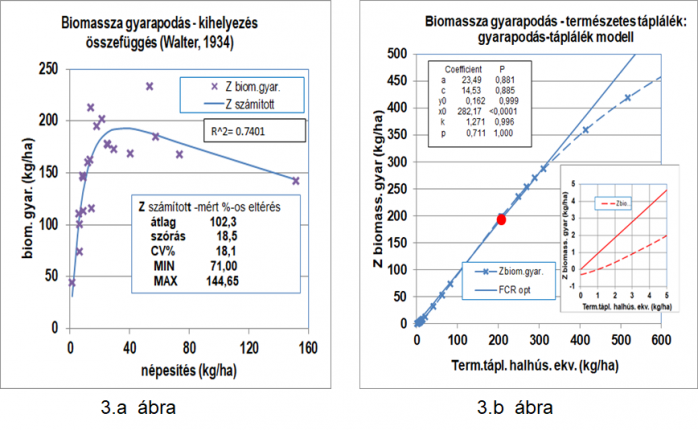
A modell eredeti ellenőrzésének szánt Walter-féle (Walter, E. 1934) magasabb számú és nagyobb szórású adatsor (közvetve mutatva 3.a ábrán), s aminek vizsgálatát 1985-ben még nem tudtunk a 6kByte RAM-os asztali számítógépen elvégezni, most elfogadhatónak látszó eredményeket adott.             
Walter 1934-es adatainak elemzésekor egy 6. „p” paramétert (a fogyasztott természetes táplálék (y₀) halhús egyenértékűségét kifejező faktort)  is bevezetve, a nem-lineáris regressziónál a

Z(N) =  - c*x+a*x*(p*y_o)^ⁿ/(p*y_o)^ⁿ+(b^ⁿ*x^ⁿ) és a
Z(N) = - c*N*w0+a* N*w0*(p*y_o)^ⁿ/(p*y_o)^ⁿ+(b^ⁿ*( N*w0)^ⁿ),

alakú egyenleteket alkalmaztuk, amelyekben Z(N) a biomassza gyarapodás az x a hektáronkénti kihelyezési mennyiség egyedszám*kezdőtömeg (N*w0) vagy kihelyezés (x) kg/ha-ban kifejezve. A „p” paraméter a lehalászott halak átlagos fehérje és energia tartalmával és a táplálék összetételével, minőségével arányos.

A nem-lineáris regressziót számítógépes programokkal végeztük, a lineáris regressziót a paraméternek tetszőleges, de megfontolt kezdeti értékeket választva, EXCEL-ben végezhető manuális iterációs eljárással is elvégeztük. A nyert nem-lineáris regressziós görbét a 3.a és 3.b ábrák mutatják be. A 2. és 3. ábrákat összevetve itt is látszik a két nézet jelleg. Bár a regresszió megbízhatósága elég gyenge (r²=0,7401) s itt csak a természetes hozam alapját képező állandó (x0=291,4 kg/ha; 3.a és 3.b ábrák) bír magas valószínűséggel (P<0,001), valamint magas magának az összefüggésnek a statisztikai biztonsága: P=0,0005.

Walter eredeti számolási módszerét nem sikerült azonosítani. Walter 64. ábrája szerinti görbe csak a 40 db/ha, illetve 994 db/ha lehalászott darabszám szerinti hozam adatokat érinti. Walter mért hozam adatokkal kapcsolatos, két különböző népesítési tartományra (0-2400, ill. 0-6000 db/ha) vonatkozó ábrájának menete sem azonos (61. és 64. ábrák; Walter, E. 1934). Lehetséges, hogy Walter „számított” görbéinek (61. és 64. sorszámú ábrák Walter közleményében) szerkesztése a Thünen-féle közgazdasági elmélet szerint, kiválasztott pontokhoz illesztett mértani sorozat alapján történt.

Az 1985-ben elemzett Péteri András által Párizsban poszteren bemutatott adatokat (Péteri A. és mtsai., 1986) is újra elemeztük, itt is alkalmazva a 6. „p” és bevezetve egy 7. ”q” paramétert (a természetes táplálék, ill. a takarmány halhús egyenértékűségét kifejező faktort).               

A „q” paraméter itt a kiadagolt takarmány (y) elfogyasztott hányadával és minőségével, valamint a lehalászott halak átlagos összetételével (fehérje, zsír, hamu stb.) arányos. Az egyenletet következő végleges formában alkalmaztuk a nem-lineáris regresszióhoz: 

Z(N) =  - c*x+a*x*(p*y_o +q*y)^ⁿ/(p*y_o +q*y)^ⁿ+(b^ⁿ*x^ⁿ)

Bár bizonyító erejű statisztikai biztonságot itt sem tudtunk elérni, a természetes hozamhoz tartozó természetes táplálékhoz tartozó P-értéknek statisztikai biztonsága (y0=1114 kg/ha, P<0,0001; itt nem bemutatott ábra) jó értéke, valamint a népesítési optimum (585 db/ha), elfogadható pontossággal jellemezte a mért hozamokat. 

A tavi vizsgálatok eredményei nem állnak ellentétben Woynárovich Elek professzor azon megállapításával, miszerint a természetes táplálék nem «egy „meglevő készlet”, hanem a vízben lefolyó biológiai termelés folyamatos terméke» (Woynarovich E. 1959), mivel a fentebb említett enzimindukció és az adaptáció révén a halak modell szerinti táplálék fogyasztása – a tenyésztési szezonra vonatkozóan összesítve – követte a vízben történő változásokat, a produkciós biológiai szinteken képződő hal táplálék termelésének dinamikáját.

A nem-lineáris regresszió ugyan nagy hibával adta meg a paraméter állandókat, de tény, hogy a mért halas adatok segítségével kifejlesztett módosított modell alkalmazható volt az 1934-es és az 1985-ben értékelt adatokra. Modellünk alapjait baktériumok esetében (Monod, J. 1941, Monod et al., 1963), majd patkányoknál (Morgan et al., 1975; Mercer, 1982; Mercer et al., 1989; stb.) és más állatoknál elméletben és gyakorlatban is igazolták. 

A haltenyésztésben, illetve a halgazdálkodásban a népesítés‑hozam összefüggéseket korábban a takarmányozás‑hozam összefüggéstől elkülönítetten vizsgálták (Nordqvist, H. 1928; Walter, 1934; Lindeman, R.L. 1942. Hutchinson, G.E. 1942; Ivlev, V.S. 1945; Maucha R. 1952). Eredményeink az eredeti, az Emil Walter által hivatkozott Nordqvist féle népesítés-hozam görbe élettani és matematikai megalapozásához járulnak hozzá és összhangban vannak az Ivlev-féle táplálék fogyasztási összefüggéssel is, illetve pontosabban annak egy éhezési taggal kiegészített változata szerinti táplálék fogyasztás‑tömeg gyarapodás összefüggéssel. Megjegyezzük még, hogy az elődjeink által megalkotott „közvetlenül kárbavesző” és „közvetve kárbavesző” táplálék fogalma (pl. Walter, 1934; Illésy, 1936; Unger, 1936; Maucha, 1952) hibás. A fogalom – a tavi optimális népesítéshez vagy maximális hozamhoz kapcsolva – azért hibás, mert még az optimális népesítésnél is van olyan takarmányozási, táplálék hasznosítási veszteség, ami „kötelezően” előfordul még a legjobb takarmány és a természetes táplálék, valamint a legmegfelelőbb népesítési, takarmányozási rendszer esetében is. A medencés nevelésnél ezek a „veszteségek” meghatározhatók és többnyire arányaikban is ismertek (Ruttkay A. 1990b).

Úgy véljük, hogy eredményeink hozzájárulnak a csak takarmányra, illetve a takarmányozott és természetes táplálék bázisra alapozott hal termelési technológiák termelésbiológiai megalapozásához. Néhány olyan következtetést is le lehet vonni, amelyek nem biztos, hogy egyeznek a halastavak hozamára vonatkozó általános elképzelésekkel.          

Továbbá, felülvizsgálhatók és értékelhetők lesznek a mai halastavi takarmányozási gyakorlat egyes technológiai és gazdaságossági hiányosságai is, s hatékonyabban használhatjuk fel azokat a haltermelő erőforrásokat, melyeket a halak, a halastavak és természetes vizek, valamint a takarmányok magukban hordoznak.

 

A modell kialakításához EU FP6-os AquaMax projekt (FOOD-CT-2006-16249) és EU FP7-es ARRAINA projekt (GA:288925) nyújtott támogatást.